图 13.1 展示美国怀俄明州黄石国家公园老忠实间歇泉喷发规律,横轴表示喷发持续时间(以分钟计),纵轴表示等待时间(以分钟计),点的亮暗程度(白到黑)代表附近点密度的高低,亮度值通过二维核密度估计方法得到,具体实现借助了 KernSmooth (Wand 和 Jones 1995) 包提供的 bkde2D() 函数,设置了喷发时间的窗宽为 0.7 分钟,等待时间的窗宽为 7分钟。不难看出,每等待55分钟左右间歇泉喷发约2分钟,或者每等待80分钟左右间歇泉喷发4.5约分钟,非常守时,表现得很老实,故而得名。说实话,二维核密度估计在这里有点大材小用了,因为数据点比较少,肉眼也能分辨出来哪里聚集的点多,哪里聚集的点少。
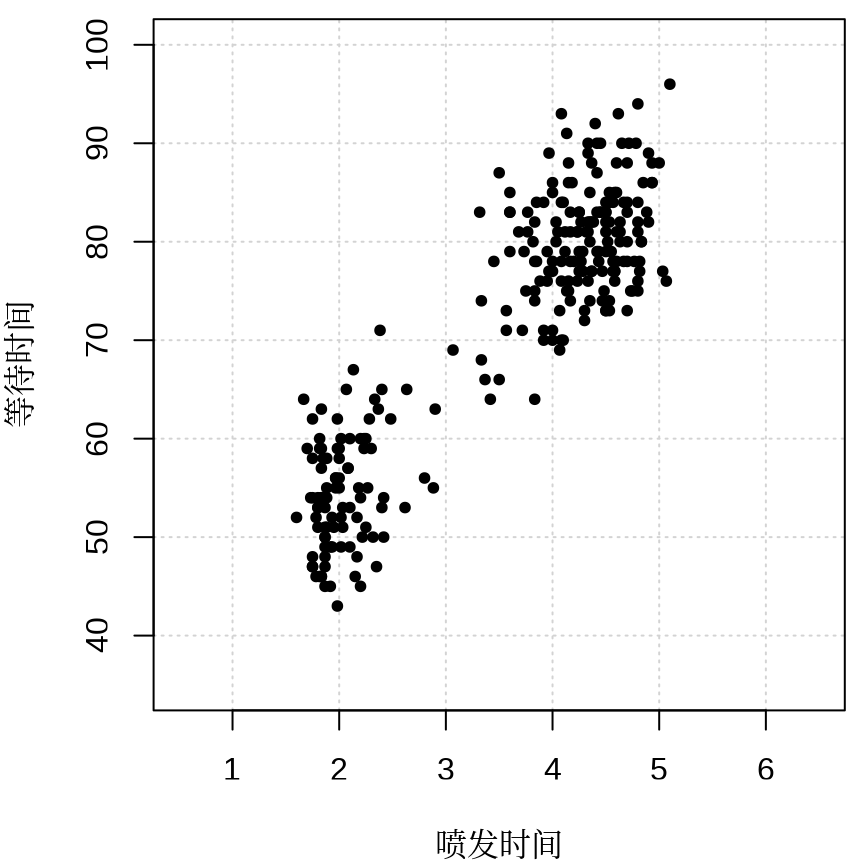
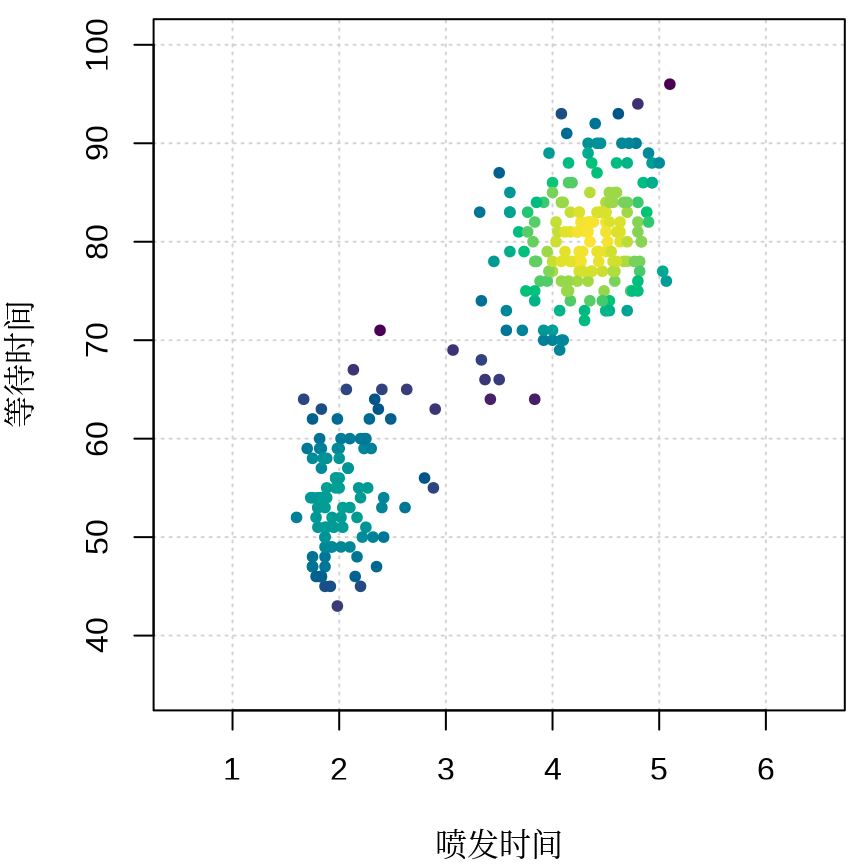
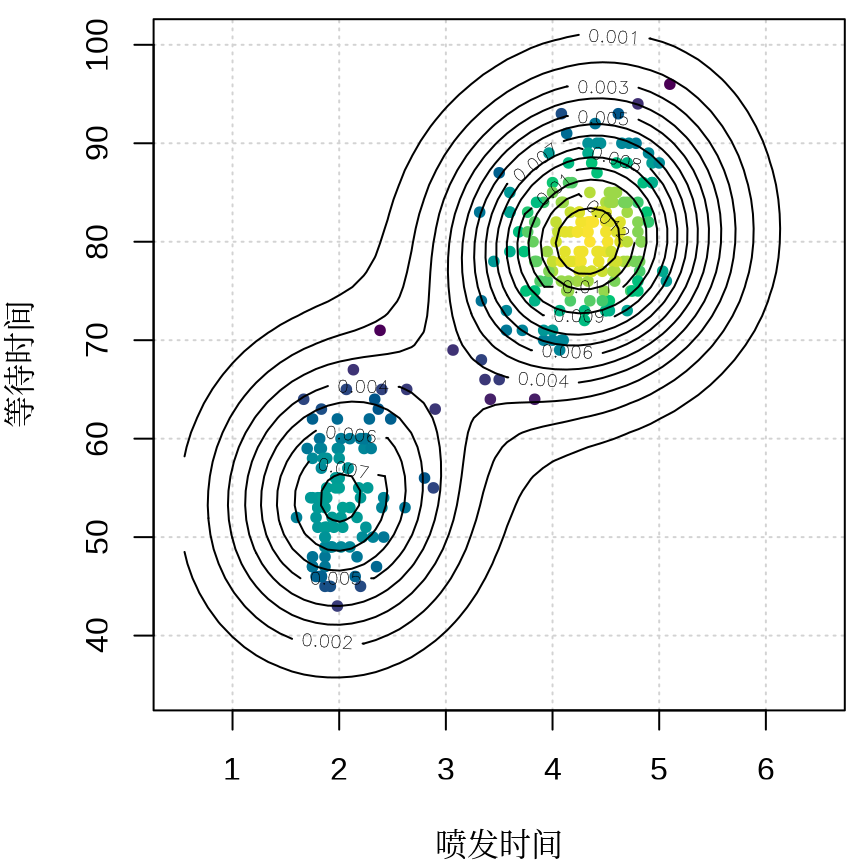
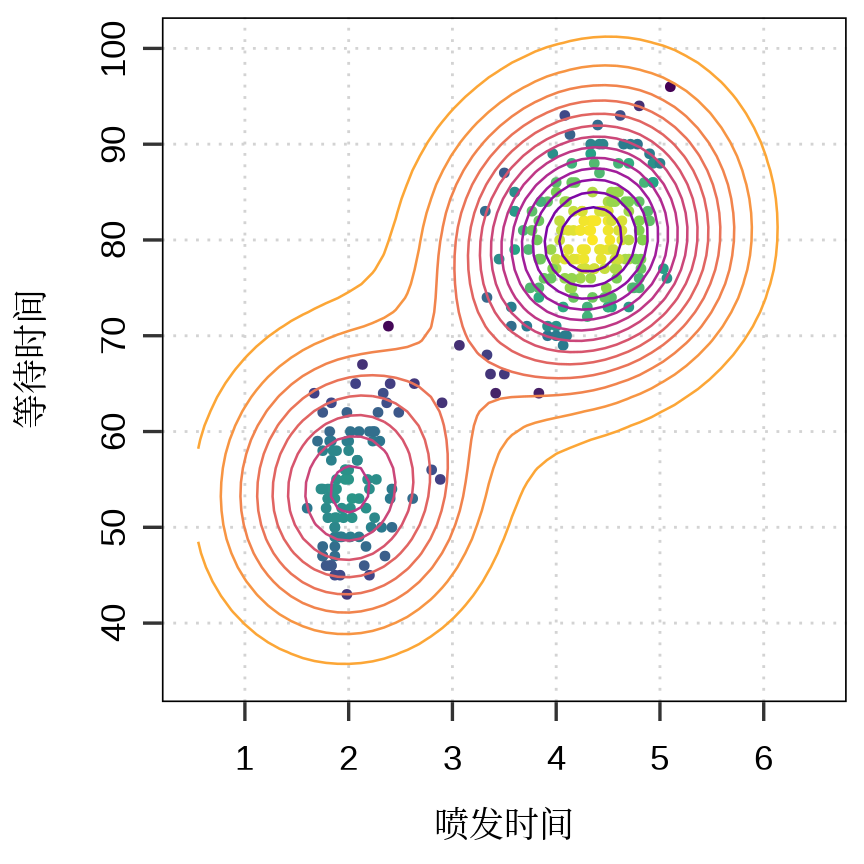
函数 bkde2D() 实现二维带窗宽的核密度估计(2D Binned Kernel Density Estimate),R 语言存在多个版本,grDevices 包的函数 densCols() 直接调用 KernSmooth 包的函数 bkde2D(),graphics 包的函数 smoothScatter() 与函数 densCols() 一样,内部也是调用 bkde2D() 函数,ggplot2 包的图层 geom_density_2d() 采用 MASS 包的函数 kde2d(),在算法实现上,MASS::kde2d() 与 KernSmooth::bkde2D() 不同,前者是二维核密度估计(Two-Dimensional Kernel Density Estimation)。
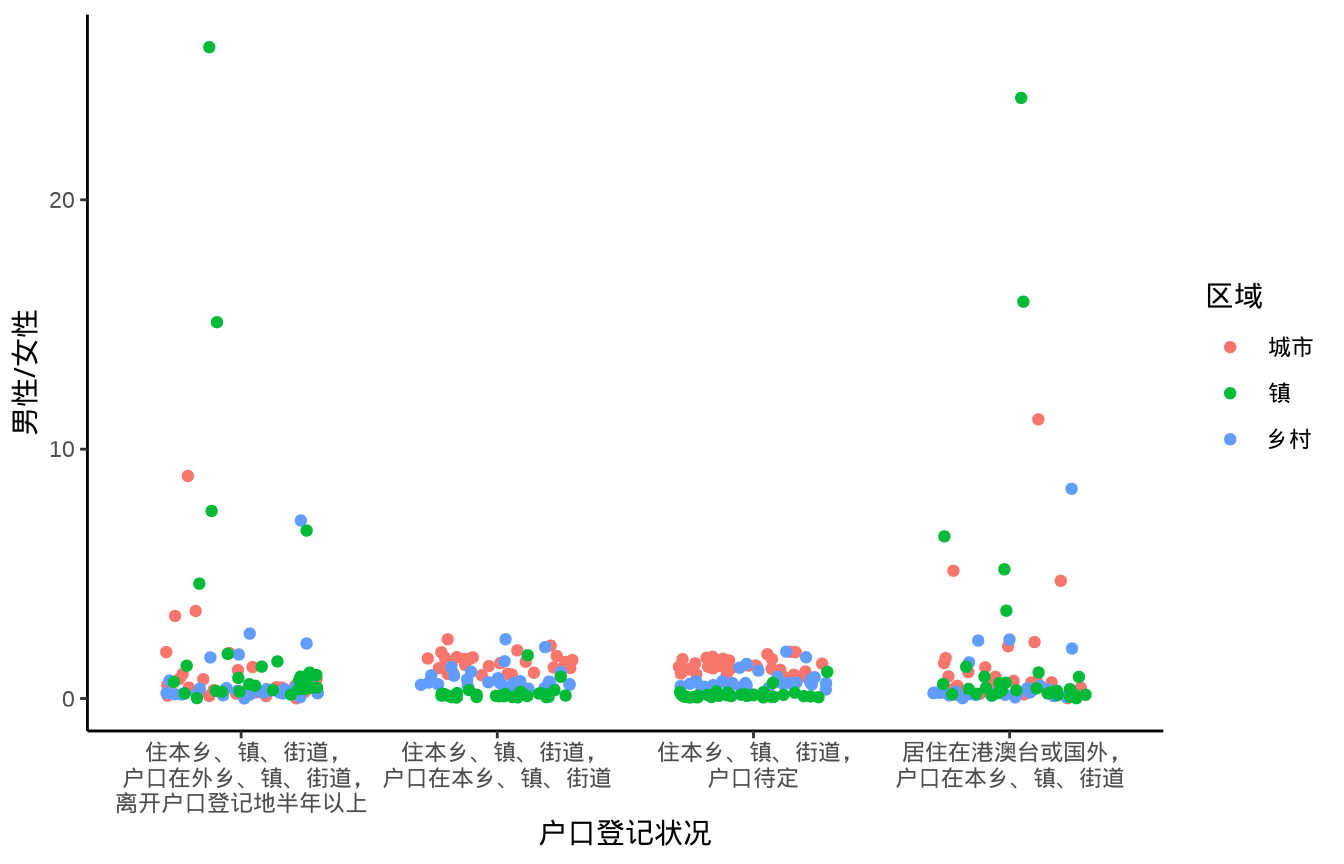
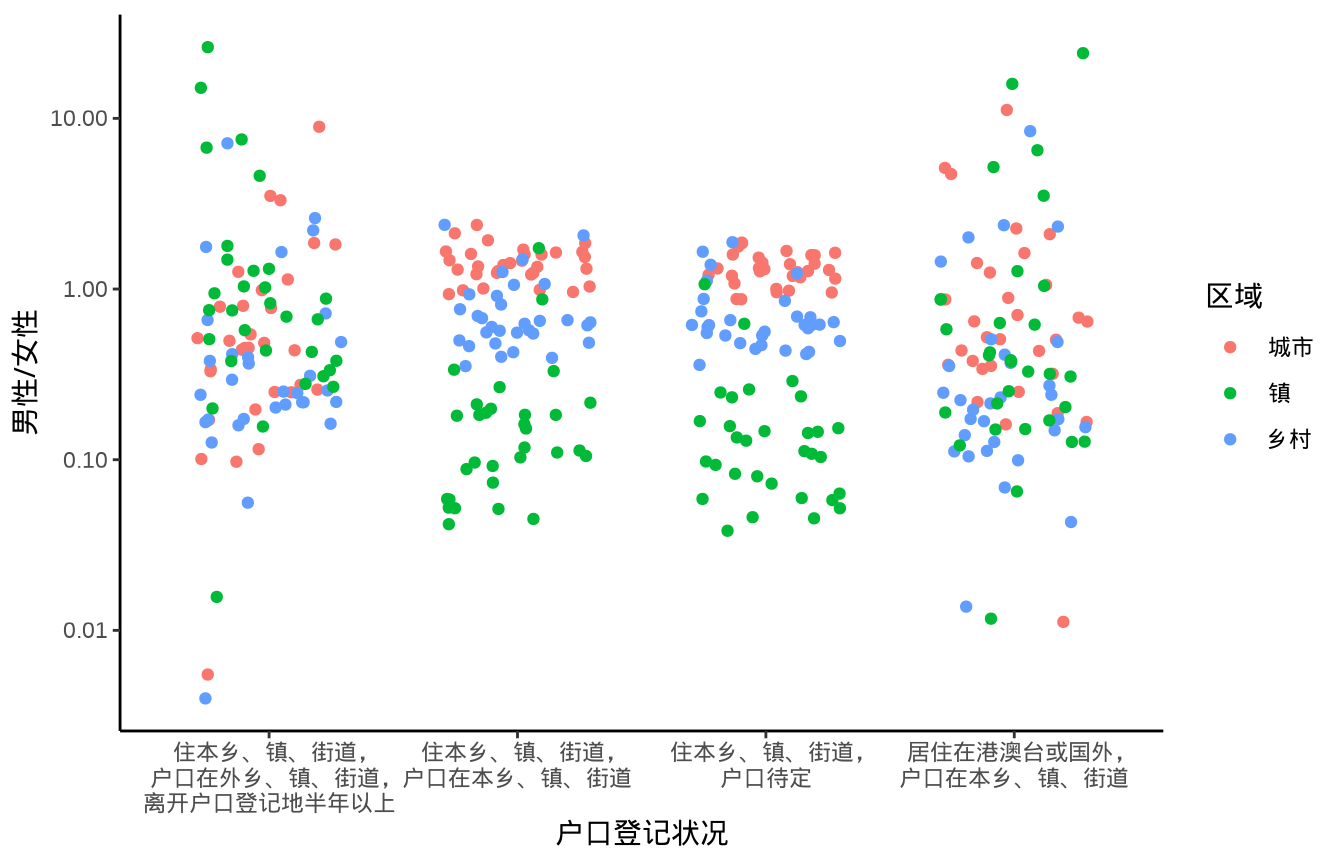
图 13.2 (a) 展示 2020 年中国各省、自治区和直辖市分城市、镇和乡村的性别比数据。数据来自中国国家统计局发布的 2021 年统计年鉴,在数据量不太大的情况下,尽可能展示原始数据,可以捕捉到更加细致的差异。社会经济相关的数据常常显示有马太效应,对原始数据适当做一些变换有利于比较和展示数据,图 13.2 (b) 展示对数变换后的性别比数据的分布。大部分地区的性别比数据都在 100:100 左右,流动人口的性别比波动大很多。


图 13.3 展示美国 1933-2020 年男性分年龄的死亡率数据1。图分上下两部分,上半部分展示死亡率原值随年龄的变化情况,以 ggplot2 默认的调色板给各个年份配色,下半部分展示死亡率对数变换后随年龄的变化情况,并以红、橙、黄、绿、青、蓝、紫构造彩虹式的调色板给各个年份配色。作图过程中,使用对数变换和调用彩虹式的调色板,帮助我们观察到更多的细节、层次。对数变换后,更加清晰地展示死亡率的变化,尤其是 0-20 岁之间的死亡率起伏变化。调用彩虹式的调色板后,约 20 年为一个阶段,每个阶段内呈现梯度变化,多个阶段体现层次性,更加清晰地展示死亡率曲线的变动趋势,透过层次看到 80 多年来,美国在医疗和公共卫生方面取得的显著改善。
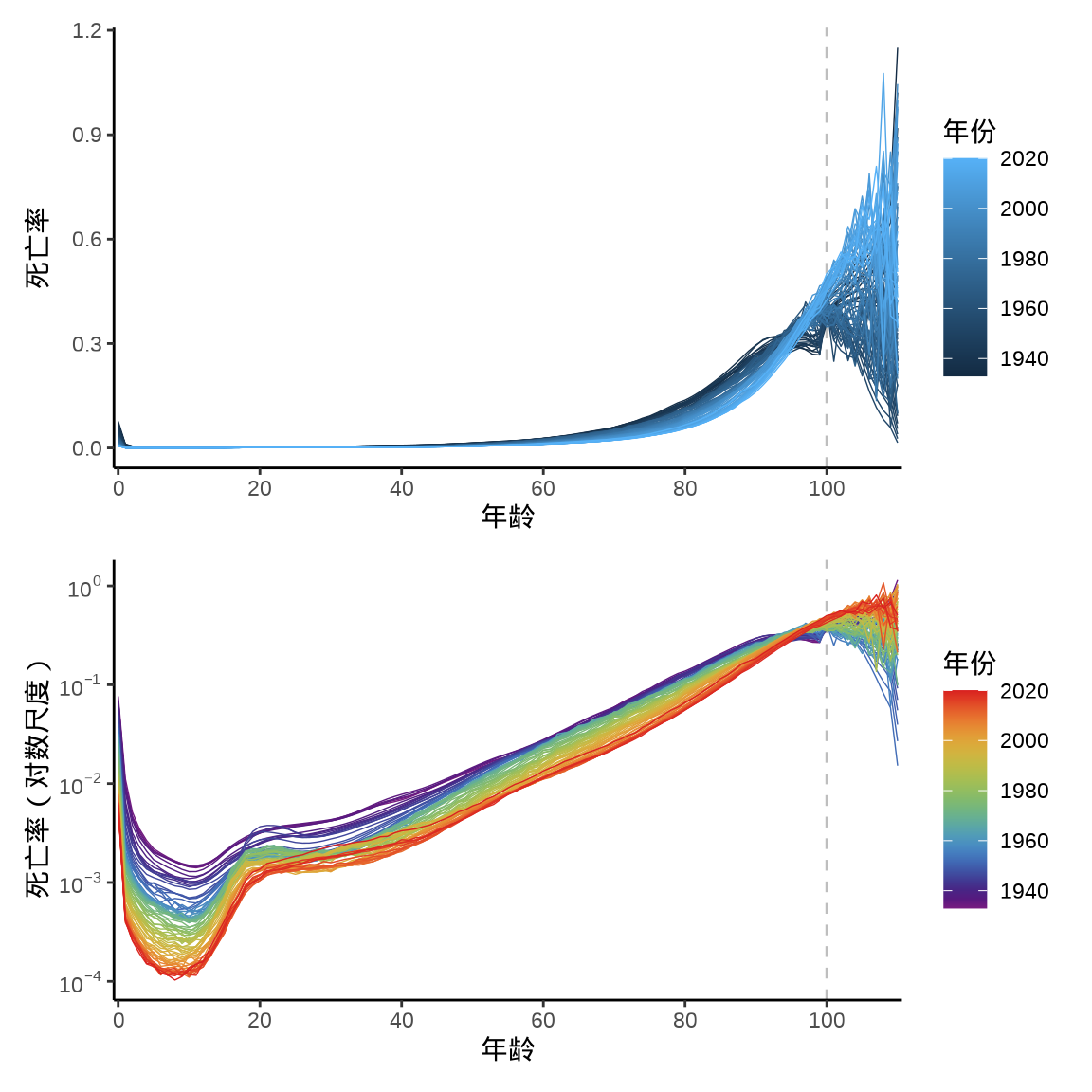
图 13.3 也展示了很多基础信息,出生时有很高的死亡率,出生后死亡率迅速下降,一直到10岁,死亡率才又开始回升,直到 20 岁,死亡率才回到出生时的水平。之后,在青年阶段死亡率缓慢增加,直至老年阶段达到很高的死亡率水平。相比于老年阶段,医疗水平的改善作用主要体现在婴儿、儿童、青少年阶段。
图 13.3 还展示了一个潜在的数据质量问题,在 100 岁之后,死亡率波动程度明显在变大,这是因为高龄人数变得很少,即死亡率的分母变得很小,分子的细小波动会被放大,也因为同样的原因,100 岁以上的死亡率主要依赖模型估计,甚至出现死亡率大于 1 的罕见情况。因此,就对比医疗和公共卫生水平的变化而言,从数据的实际情况出发,100 岁以上的情况可以不参与比较。
图 13.4 死亡率数据是对数尺度
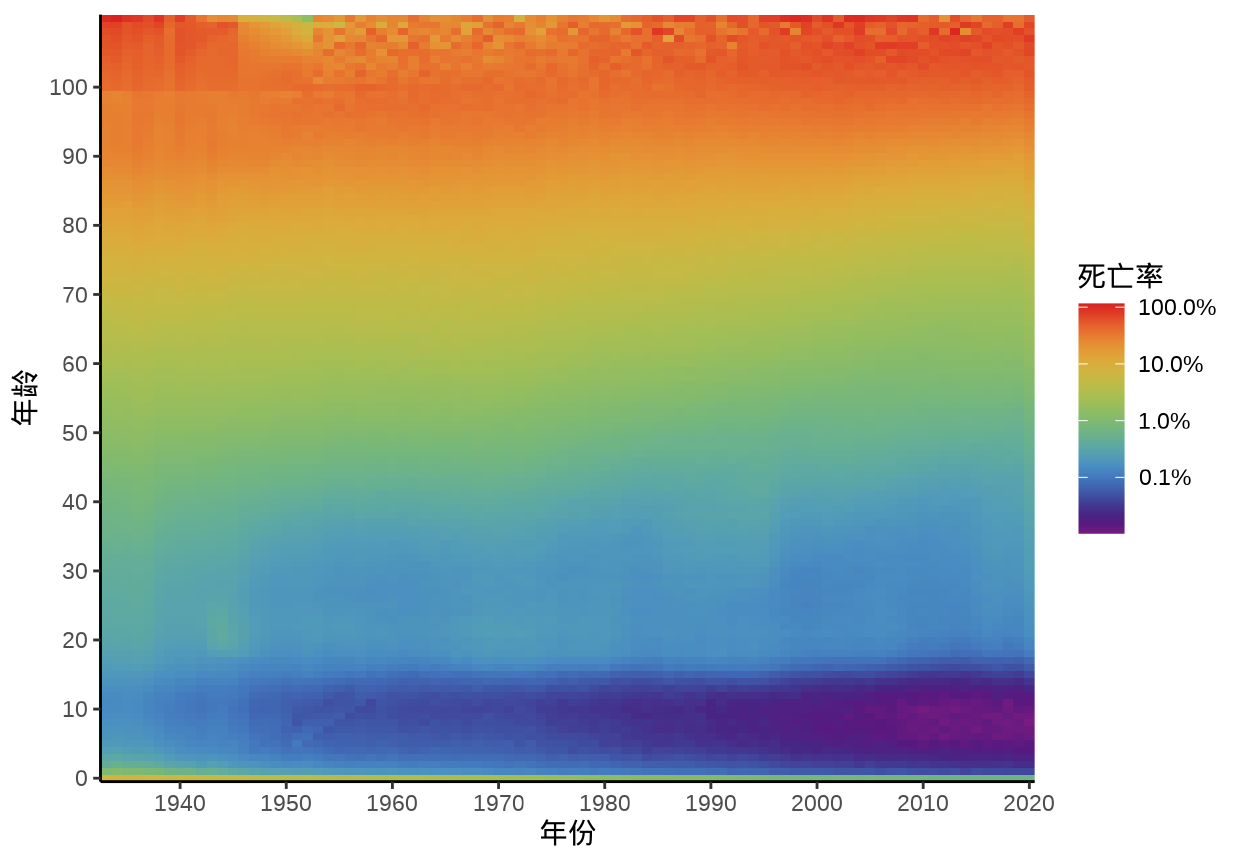
更加深入的分析和建模,详见 Marron 和 Dryden (2022) 的第一章。
VADeaths 数据来自 Base R 内置的 datasets 包,记录 1940 年美国弗吉尼亚州死亡率,如下表。
| 农村男 | 农村女 | 城市男 | 城市女 | |
|---|---|---|---|---|
| 50-54 | 11.7 | 8.7 | 15.4 | 8.4 |
| 55-59 | 18.1 | 11.7 | 24.3 | 13.6 |
| 60-64 | 26.9 | 20.3 | 37.0 | 19.3 |
| 65-69 | 41.0 | 30.9 | 54.6 | 35.1 |
| 70-74 | 66.0 | 54.3 | 71.1 | 50.0 |
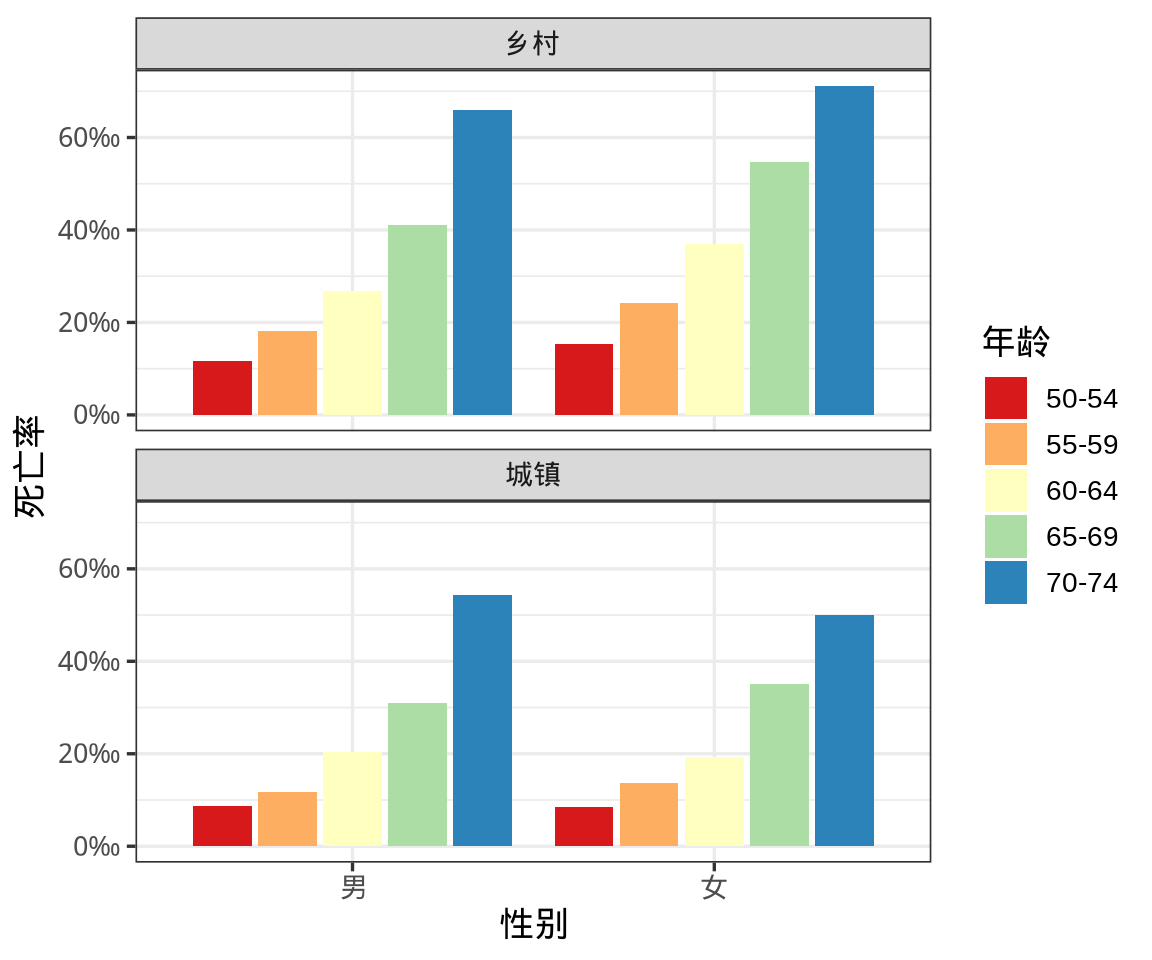
死亡率数据是按年龄段、城乡、性别分组统计的,这是一个三因素交叉统计表,表格中第1行第1列的数据表示 50-54 岁乡村男性的死亡率为 11.7 ‰ ,即在 50-54 岁乡村男性群体中,1000 个人中死亡 11.7 个,这是抽样调查出来的数字。下图分年龄段、城乡、性别展示弗吉尼亚州死亡率数据,从图例来看,突出的是各年龄段的对比,图主要传递的信息是各年龄段的死亡率差异。无论城市还是乡村,也无论男性还是女性,年龄越大死亡率越高,这完全是一个符合生物规律的客观事实,这是众人皆知的,算不上洞见。
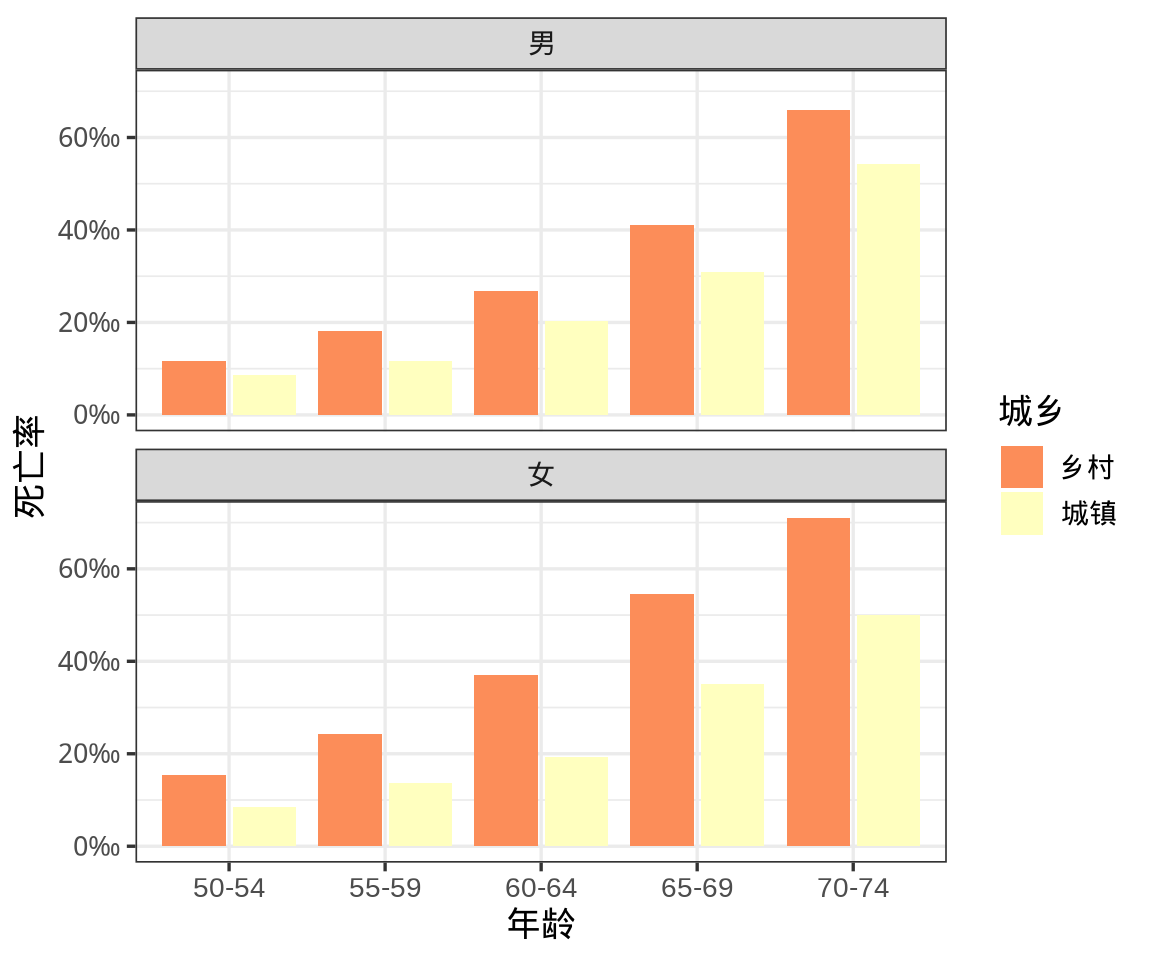
将对比对象从年龄段转变为城乡,描述城乡差距在死亡率上的体现,是不是一下子更深刻了呢?城市降低各个年龄段的死亡率,暗示着城市的居住条件、医疗水平比乡村好,提高城市化率增加全民的寿命。严格来说,就这个粗糙的数据集不能如此快地下这个结论,但是,它暗示这个信息,同样也符合人们的常识。
不失一般性,考虑连续随机变量的条件分布和累积分布。不妨设随机变量 \(x\) 的概率分布函数和概率密度函数分别是 \(F(x)\) 和 \(f(x)\) 。已知概率分布函数和概率密度函数之间有如下关系。
\[ F(x) = \int_{-\infty}^{x} f(t) \mathrm{dt} \]
数据可视化陷阱 (Pu 和 Kay 2020)
diamonds 数据来自 ggplot2 包,记录了约 54000 颗钻石的价格、重量、切工、颜色、纯净度、尺寸等属性信息。如何表达条件分布和累积分布,在这个示例中,应该用条件分布还是累积分布。
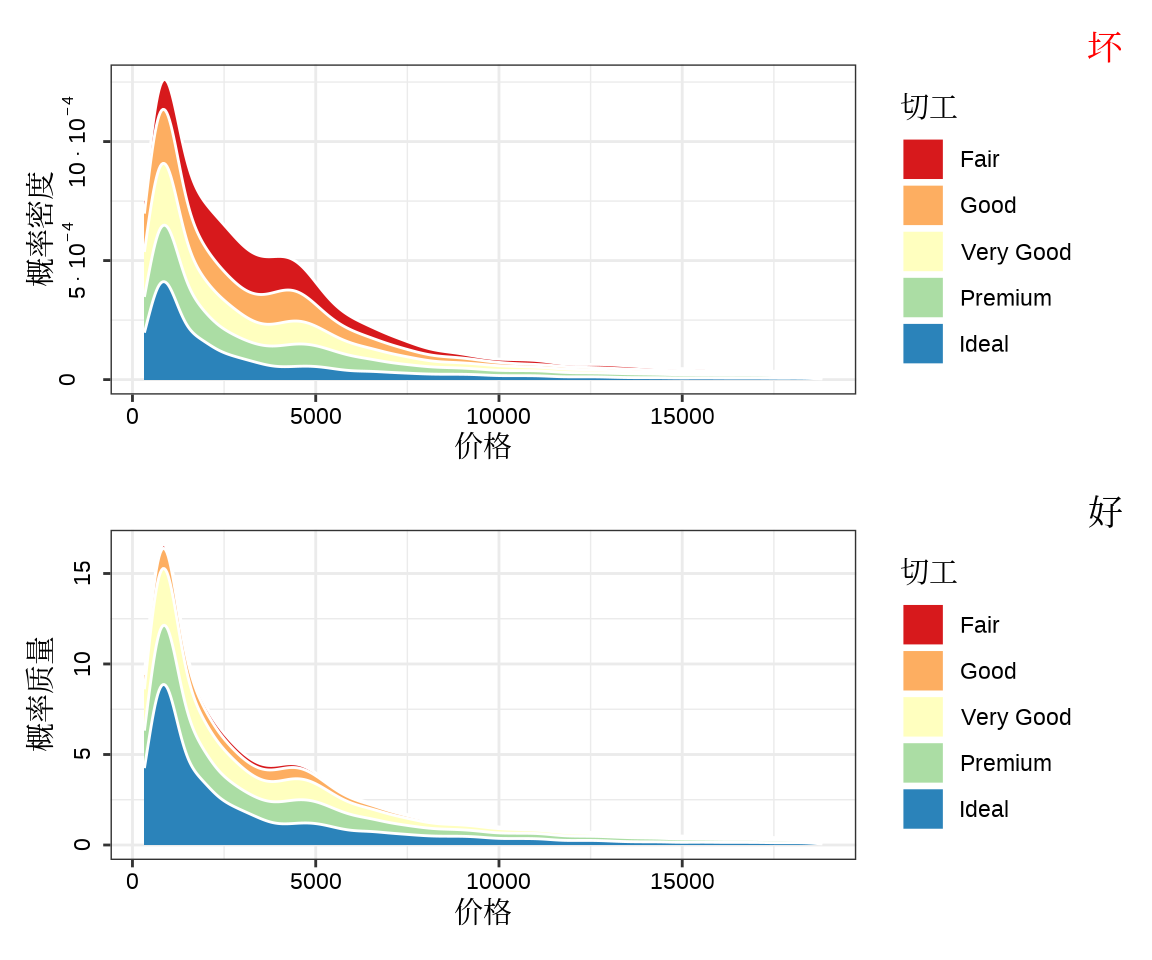
0 和 1 是世界的原点,蕴含大道真意,从 0-1 分布也叫伯努利分布,独立同 0-1分布之和可以衍生出二项分布。在一定条件下,可以用泊松分布近似二项分布。根据中心极限定理,独立同二项分布的极限和与正态分布可以发生关系。在二项分布、正态分布的基础上,可以衍生出超几何分布、贝塔分布等等。本书多个地方以二项分布为例介绍基本统计概念和模型。
在给定置信水平为 0.95,即 \(\alpha = 0.05\),固定样本量 \(n = 10\),观测到的成功次数 \(x\) 可能为 \(0,1,\cdots,10\)。对于给定的 \(p\),不同 \(x\) 值出现的机率 \(P(X = x)\) 由 \((p + q)^{10}\) 二项展开式的项给出,这里 \(q = 1-p\),即:
\[ P(X = x) = \binom{n}{x}p^x(1-p)^{n-x} \tag{13.1}\]
在给定 \(p = 0.1\) 的情况下,求二项分布的上 \(\alpha/2 = 0.025\) 分位点,尾项之和不应超过 \(\alpha/2\),最大的 \(x\) 值可有如下方程给出:
\[ \sum_{r = x}^{n}\binom{n}{x}p^x(1-p)^{n-x} = \frac{\alpha}{2} \tag{13.2}\]
在 R 语言中,函数 qbinom() 可以计算上述二项分布的上分位点 \(x = 3\),即
反过来,若已知上分位点为 \(x = 3\),则概率为
\[ P(X > 3) = \sum_{x > 3}^{10}\binom{10}{x}0.1^x*(1-0.1)^{10-x} \tag{13.3}\]
在 R 语言中,函数 pbinom() 可以计算上述二项分布的上分位点对应的概率为 \(0.0127952\)。
首先简单回顾一下置信区间,在学校和教科书里,有两种说法如下:
为什么要采纳第一种说法而不是第二种呢?这其实涉及到置信区间的定义问题,历史上 E. S. Pearson 和 R. A. Fisher 曾有过争论。和大多数以正态分布为例介绍参数的置信估计不同,下面以二项分布为例展开介绍。我们知道二项分布是 N 个伯努利分布的卷积,而伯努利分布又称为 0-1 分布,最形象的例子要数抛硬币了,反复投掷硬币,将正面朝上记为 1,反面朝上记为 0,记录正反面出现的次数,正面朝上的总次数又叫成功次数。
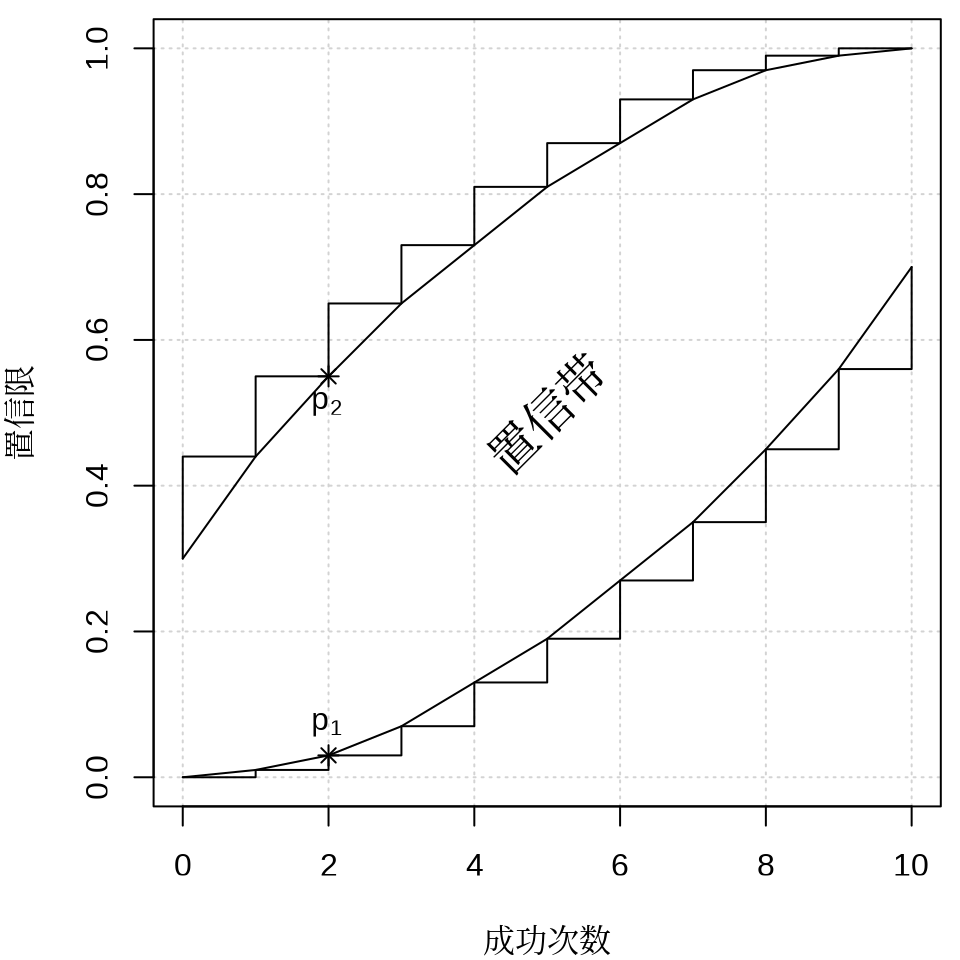
1934 年 C. J. Clopper 和 E. S. Pearson 在给定置信水平 \(1- \alpha = 0.95\) 和样本量 \(n = 10\) 的情况下,给出二项分布 \(B(n, p)\) 参数 \(p\) 的区间估计(即所谓的 Clopper-Pearson 精确区间估计)和置信带 (Clopper 和 Pearson 1934),如 图 13.8 所示,横坐标为观测到的成功次数,纵坐标为参数 \(p\) 的置信限。具体来说,固定样本量为 10,假定观测到的成功次数为 2,在置信水平为 0.95 的情况下,Base R 内置的二项精确检验函数 binom.test(),可以获得参数 \(p\) 的精确区间估计为 \((p_1, p_2) = (0.025, 0.556)\),即:
#>
#> Exact binomial test
#>
#> data: 2 and 10
#> number of successes = 2, number of trials = 10, p-value = 1
#> alternative hypothesis: true probability of success is not equal to 0.2
#> 95 percent confidence interval:
#> 0.02521073 0.55609546
#> sample estimates:
#> probability of success
#> 0.2值得注意,这个估计的区间与函数 binom.test() 中参数 p 的取值无关,也就是说,当 \(p = 0.4\),区间估计结果是一样的,如下:
#>
#> Exact binomial test
#>
#> data: 2 and 10
#> number of successes = 2, number of trials = 10, p-value = 0.3335
#> alternative hypothesis: true probability of success is not equal to 0.4
#> 95 percent confidence interval:
#> 0.02521073 0.55609546
#> sample estimates:
#> probability of success
#> 0.2由此,也可以看出区间估计与假设检验的一些关系。
统计图形很重要的一个作用是解释统计概念,这就要求不拘泥于抽象的严格数学表达,借助数值模拟,可视化等手段帮助读者发散思维,加深理解复杂的逻辑概念,建立统计直觉,正如顾恺之所言「以形写神,形神兼备」。下面仅以二项分布为例讲讲区间估计及其覆盖概率。众所周知,在置信水平为 \(1 - \alpha\) 的情况下,二项分布 \(\mathrm{Bin}(n,p)\) 的参数 \(p\) (也叫成功概率)的 Wald 区间估计为
\[ (\hat{p} - Z_{1-\alpha/2} \sqrt{\hat{p}*(1-\hat{p})/n}, \hat{p} + Z_{1-\alpha/2} \sqrt{\hat{p}*(1-\hat{p})/n}) \tag{13.4}\]
其中,\(n\) 为样本量,\(Z_{1-\alpha/2}\) 为标准正态分布 \(\mathcal{N}(0,1)\) 在 \(1-\alpha/2\) 处的分位点。 \(\alpha\) 一般取 0.05,进而 \(Z_{1-\alpha/2} \approx 1.96\)。用通俗的话说,有 \(1 - \alpha\) 的把握确定参数真值 \(p\) 在该估计区间内。可见区间估计的意义是解决点估计可靠性问题,但是可靠性和精度往往不能兼得。统计上,通常的做法是先给定可靠性,去尽可能提升精度,即给定置信水平,使估计区间的长度尽可能短,这就涉及到区间估计的方法问题。
下面通过数值模拟的方式辅助说明 Wald 和 Agresti-Coull 两种区间估计方法,现固定样本量 \(n = 10\) 或 \(n = 100\),重复抽样 1000 次,将参数 \(p\) 以 0.01 的间隔离散化,从 0.01 取值到 0.99。已知给定参数 \(p\),每次抽样都可以得到参数 \(p\) 的估计值 \(\hat{p}\) 及其置信区间,1000 次的重复抽样可以计算出来 1000 个置信区间,每个区间要么覆盖真值,要么没有覆盖真值,覆盖的比例可以近似为覆盖概率。
如 图 13.9 所示,从上往下分别代表 Wald、 Agresti-Coull、 Wilson 和 Clopper-Pearson 区间估计,纵坐标是覆盖概率,横坐标是参数 \(p\) 的真值,图中黑虚线表示置信水平 \(1-\alpha=0.95\),红、蓝点线分别表示样本量 \(n=10\) 和 \(n=100\) 的模拟情况。不难看出,Wald 区间估计方法在小样本情况下表现很差,覆盖概率很少能达到置信水平的,而 Agresti-Coull 区间估计在 Wald 基础上添加了修正后,情况得到显著改善。更多区间估计方法的详细比较见文献 Blyth 和 Hutchinson (1960);Brown, Cai, 和 DasGupta (2001);Geyer 和 Meeden (2005) 。
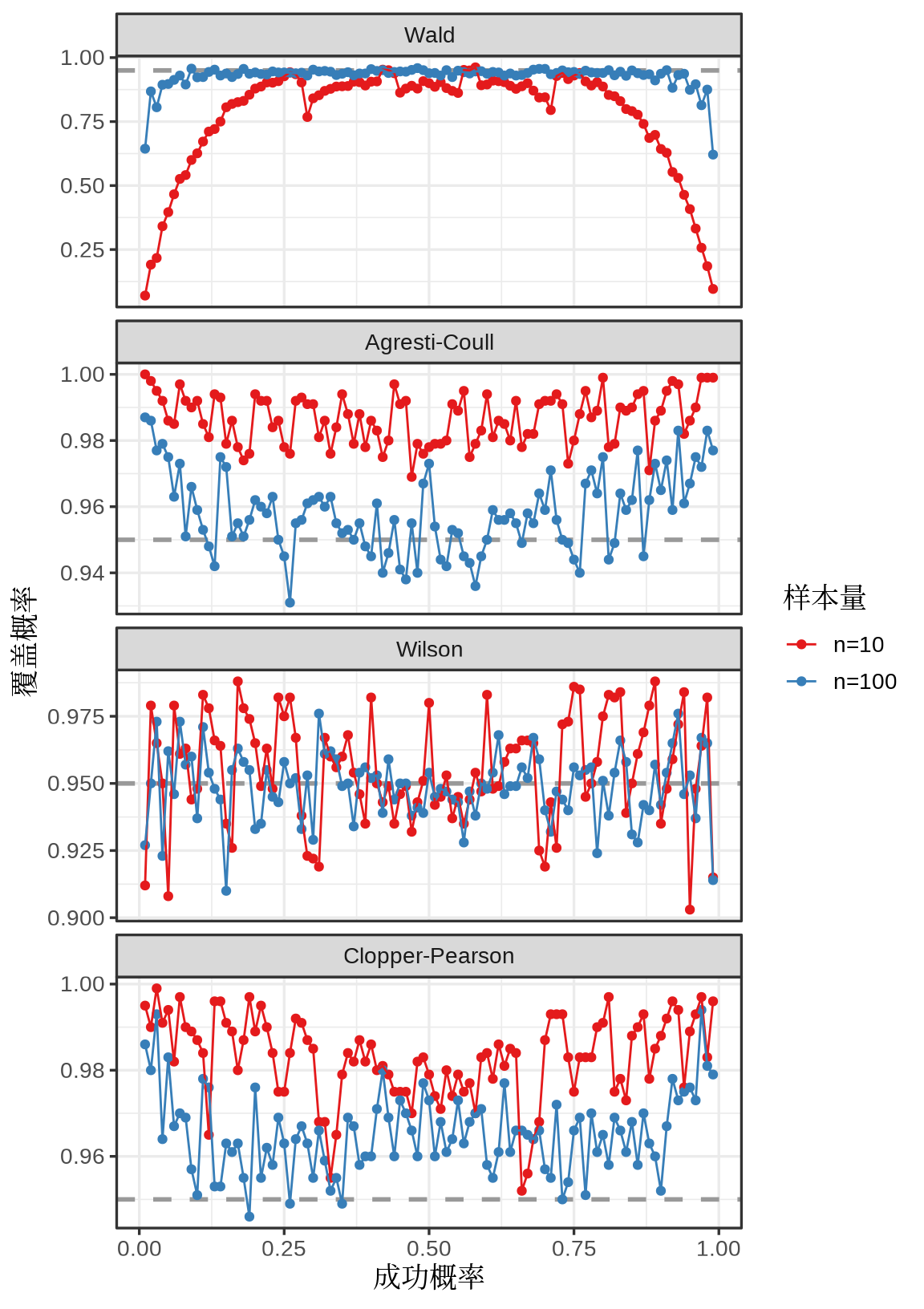
通过 图 13.9 一看就明白了几种区间估计方法的优劣,以及为什么软件普遍默认采用 Wilson 估计方法?因为它又稳定又准确。 Wilson 区间估计用的更加广泛的,Base R 内置的比例检验函数 prop.test() 在不启用 Yates 修正时,就是用该方法获得比例 \(p\) 的区间估计 (Wilson 1927)。Clopper-Pearson 区间估计特别适合小样本情形,它是精确区间估计方法,Base R 内置的二项比例检验函数 binom.test() 就是用该方法获得比例 \(p\) 的区间估计(Clopper 和 Pearson 1934)。
请读者再思考两个问题: 图 13.9 为什么呈现对称的形式,泊松分布会和二项分布有类似的现象吗?如果有的话,连续分布,如正态分布和指数分布也会有吗?